Real-World Cryptography

암호학의 기본 개념부터 최신 기술 동향까지, 어플리케이션 개발 실무에 필요한 핵심 내용을 알기 쉽게 정리했습니다.

Contents


배경

업무를 하다보면 암복호화를 사용해야 할 일들이 종종 있다. 각 언어에 구현된 라이브러리를 사용하는 것은 복잡하지 않지만, 각 암호화가 내부적으로 어떠한 방식으로 진행되는지는 알지 못했다. 결정적으로 이 책을 읽게 된 계기는 CryptoJS 와 OpenSSL 인코딩 와 같은 일들을 겪으면서, 암호학에 대해 좀 더 많은 지식을 얻고 싶어서 읽게 되었다. 책에서는 암호학에 대한 다양한 설명들이 있지만, 이 글에서는 어플리케이션 개발을 위한 실무 중심의 정리를 해보려 한다.


암호학의 분류

암호학 알고리즘들을 다양한 기준으로 분류할 수 있지만, 크게 다음과 같은 기준들로 쉽게 분류할 수 있다. 먼저 비밀의 공개여부를 기준으로 다음과 같이 나눌 수 있다.

| 대칭 암호학 | 비대칭 암호학 | | --- | --- | | 비밀 하나가 사용된다. 여러 참가자가 비밀을 알고 있는 경우, 이는 공유된 비밀이 된다. 비밀키 암호화라고도 불린다. | 참가자들은 비밀에 대해 비대칭적인 관점을 가지고 있다. 예를 들어 일부는 공개키를 알고 있고, 일부는 공개 키와 비밀 키 모두를 알고 있다. 공개 키 암호화 라고도 불린다. |

또한, 암호학 알고리즘 자체를 기준으로 분류해 볼 수 있다.

| 수학 기반 구성 | 휴리스틱 기반 구성 | | --- | --- | | 인수 분해와 같은 수학적 문제에 의존한다. (ex. 전자서명 및 비대칭 암호화를 위한 RSA 알고리즘) | 암호 분석가의 관찰 및 통계 분석에 의존한다 (대칭 암호화를 위한 AES 알고리즘) |


해시 함수

해시 함수의 역할은 명료하다. 모든 값에 대한 고유한 식별자를 붙이는 것이다. 해시는 다양한 방법에서 사용될 수 있다. 가장 친숙하게 사용되는 예시는 hashsum 이다. (Linux Mint) ISO 이미지 검증하기 문서를 예시로 보면, Linux Mint OS 파일의 바이너리 해시값을 담은 파일 sha256sum.txt 와 실제 다운로드된 파일의 sha256 hashsum 을 비교한다. 만약 둘의 해시값이 다르다면, ISO 파일 다운로드에 이상이 생긴 것으로 판단할 수 있다. 해시 함수의 결과값을 다이제스트(digest), 체크섬(checksum) 으로 표현하기도 한다.

해시 함수는 다음의 성질들을 만족해야 한다.

| 속성 | 설명 | | --- | --- | | 역상 저항성(pre-image resistance) | 주어진 출력을 입력으로 바꾸는 역함수를 만들 수 없다. | | 제2 역상 저항성(second pre-image resistance) | 하나의 해시 함수의 출력을 만들 수 있는 입력은 하나만 존재한다. | | 충돌 저항성(collision resistance) | 같은 출력값을 만들 수 있는 입력값은 하나뿐이다. |


과거에는 MD5, SHA-1 등의 해시 함수를 사용했지만, 최근에 두 해시 함수는 모두 뚫렸다. 최근에 자주 사용되는 해시 알고리즘으로는 SHA-2, SHA-3 가 대표적이다.



SHA-2

가장 널리 채택된 해시 함수는 SHA-2(Secure Hash Algorithm 2) 이다. 우리가 흔히 말하는 SHA-256, SHA-512 는 모두 SHA-2 계열의 해시 함수이다. SHA-2 에는 SHA-224, SHA-256, SHA-384, SHA-512 알고리즘이 있다. 뒤에 붙은 숫자는 출력의 비트수를 의미한다. SHA-2 함수에서는 Davies-Meyer 압축 함수가 사용된다. Davies-Meyer 압축 함수는 블록 암호(block cipher) 에 의존한다.

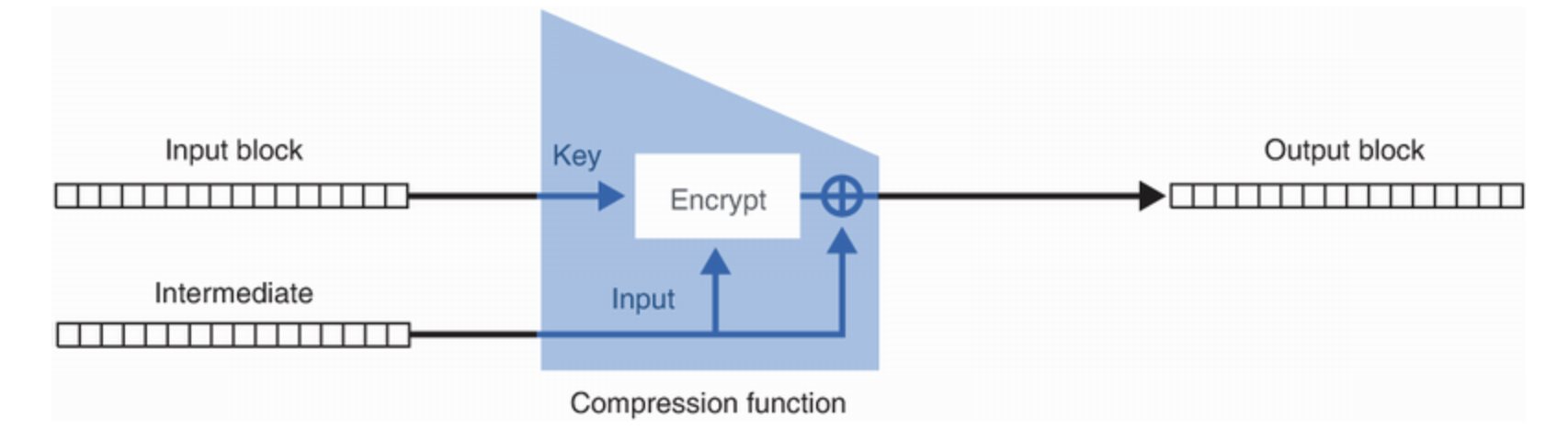
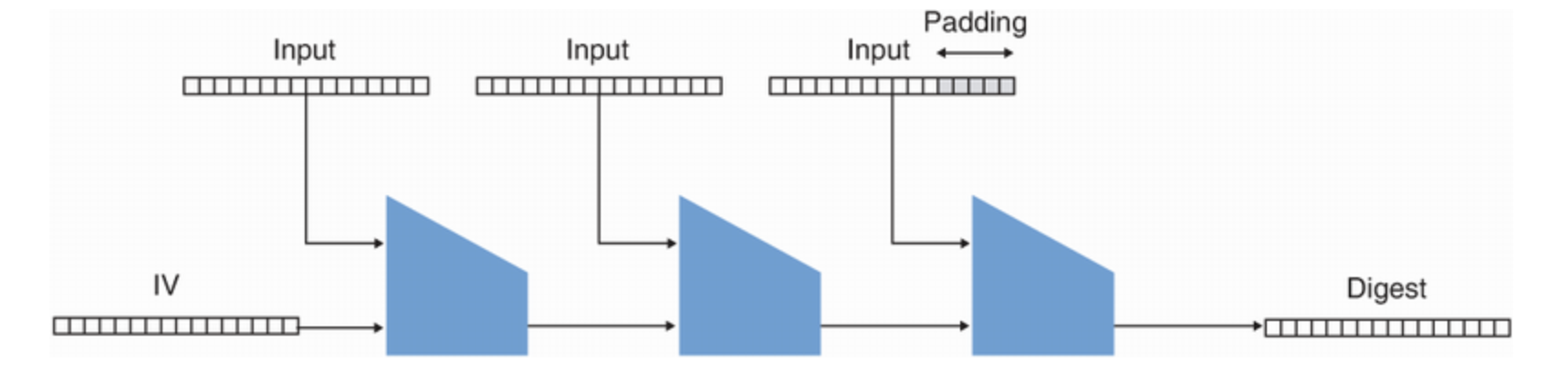
SHA-2 는 위의 그림과 같은 함수를 반복적으로 호출하는 알고리즘인 머클-담고르(Merkle-Damgard) 구조이다. 구체적으로는, 다음의 두 단계를 거쳐 작동한다.

  1. 해시하려는 입력에 패딩을 적용한 다음, 다음 입력을 압축 함수에 맞는 블록으로 자른다. 만약 블록 크기보다 데이터의 크기가 작다면, 패딩을 통해 특정 바이트를 추가한다.
  2. (1) 의 출력을 압축 함수의 두 번째 인수로 사용하여 압축 함수를 메세지 블록에 반복적으로 적용한다. 다만, 첫 번째 압축의 경우, 압축 함수의 인자가 하나밖에 없는데, 이를 위해 초기화 벡터(IV) 를 추가한다.



SHA-3

앞에 간략히 정리한 대로, MD5, SHA-1 는 모두 보안적으로 뚫린 해시 알고리즘이다. 이 두 알고리즘은 모두 머클-담고르 구조를 사용했다. NIST 에서는 보다 더 안전한 해시 알고리즘을 위해 공개 대회를 열었고, 2015년에 SHA-3 라는 알고리즘이 표준화되었다. SHA-3 는 머클-담고르와는 다른 구조인 스펀지 구조 (sponge construction) 으로 제작되었다. 구체적으로, SHA-3 는 keccak-f 라는 순열 함수를 기반으로 작동한다.

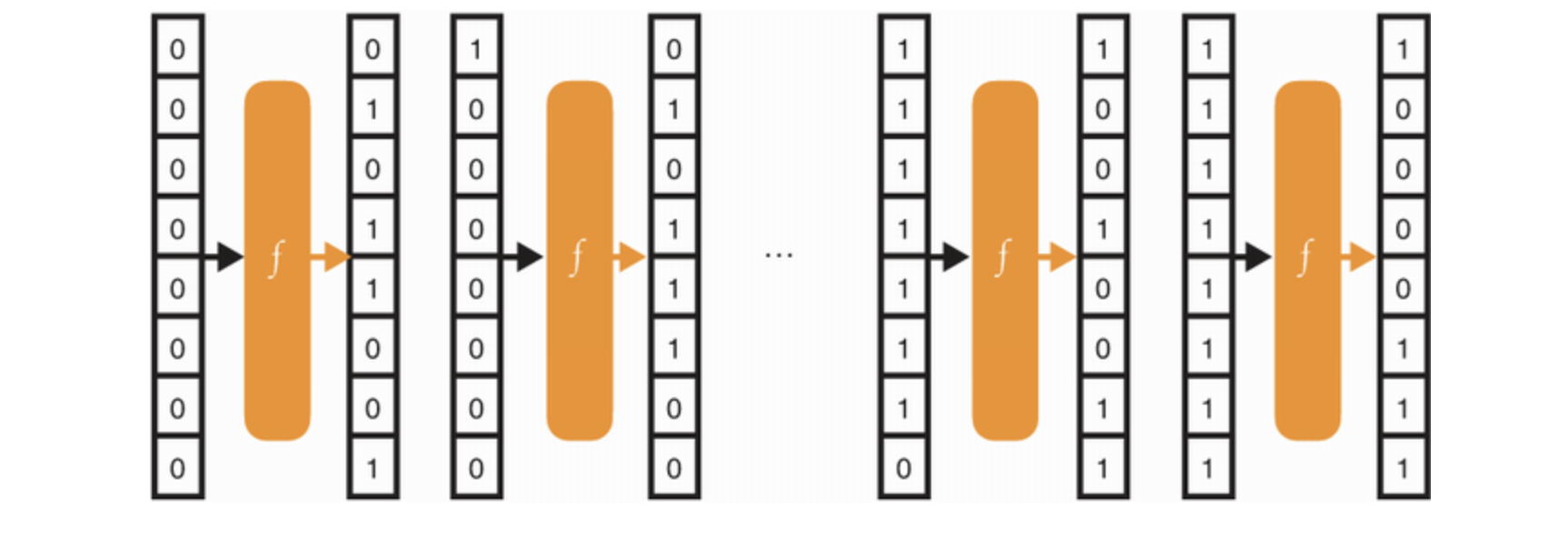
순열 함수 내부의 동작원리는 블랙박스로 내버려 두고, 간단하게 8비트의 데이터를 다른 8비트로 대체했다고 생각할 수 있다. 여기에 더하여, 8비트를 r(rate) 와 c(capacity) 로 나눈다. 여기서, c 는 비밀로 취급해야 하며 c 가 클수록 스펀지 구조가 더 안전하다고 한다. 해시를 위해서는 순열 입력의 r 과 입력을 XOR 하면 된다.

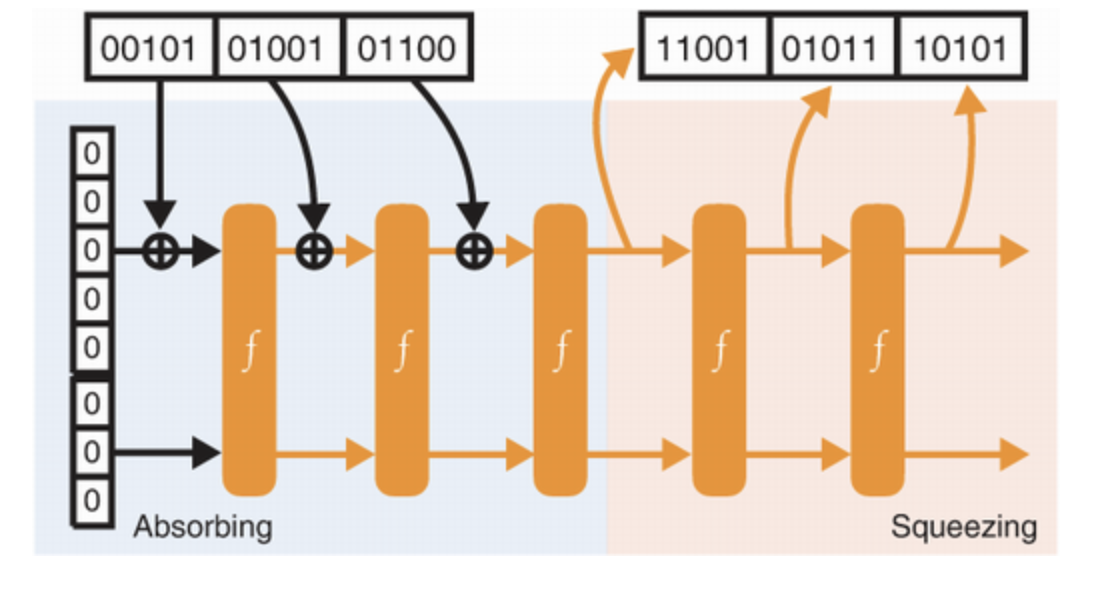
SHA-3 은 다음의 로직을 반복적으로 적용한다.

  1. 필요한 경우 입력에 패딩을 추가하고, 입력을 r만큼의 크기의 블록으로 나눈다.
  2. 순열 입력으로 각 블록을 XOR하고 각블록이 XOR 된 후 상태를 순열하면서 순열 함수를 반복적으로 호출한다.
  3. 다이제스트를 얻기 위해서는, (1), (2) 의 로직을 반복적으로 적용하며 r 의 값을 읽어들인다.

SHA-3 스펀지 로직에서는 반복하여 순열 함수를 호출하는 과정을 absorb, digest 를 구하는 과정을 squeeze 라고 부른다.



메시지 인증 코드

해시 함수와 비밀키를 혼합하면 데이터 무결성을 보호하기 위한 암호학 프리미티브인 메시지 인증 코드(Message Authentication Code) 를 얻을 수 있다. 단순하게 MAC 코드를 생성하기 위해서는, 검증하고자 하는 값 앞에 비밀키를 붙여서 해시하면, 일종의 MAC 을 도출할 수 있다. MAC 의 일반적인 보안 목표는 새 메세지의 인증 태그 위조(Authentication Tag Forgery) 를 방지하는 것이다. 즉, 비밀 키 k 를 모르면 위조하고자 하는 메세지 m 에 대한 인증 태그 t = MAC(k, m) 을 계산할 수 없음을 의미한다. 해시 함수의 역상 저항성 을 통해 안전한 MAC 을 만들 수 있지만, 단순한 MAC 로직을 구현한다면 해커들의 리플레이 공격 을 받을 수 있다.



리플레이 공격

MAC 함수는 해시와 비밀키로 이루어져 있기 때문에, 해시 함수의 역상 저항성으로 인해 MAC Message 를 원본 메세지로 구하는 MAC 역함수는 구하기 힘들다. 하지만, 암호화한 MAC 값을 그대로 기록해 두었다 다시 사용하면 보안적으로 위험해질 수 있다. 리플레이 공격은 MAC 외에, 일반적인 API 들에도 모두 적용된다.

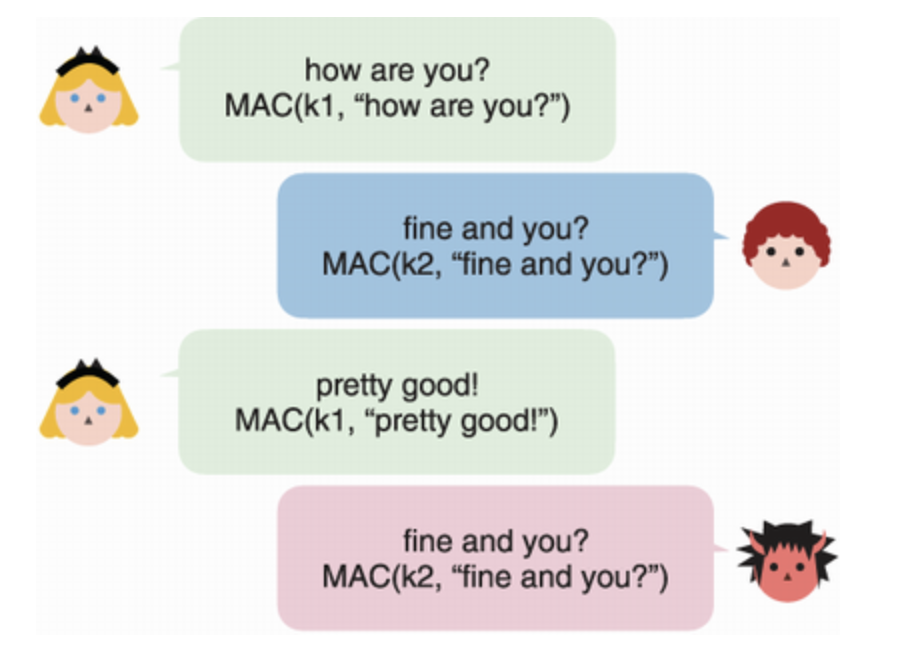
위의 그림과 같이, MITM 이 앞의 MAC 해시를 그대로 사용하면, 보안 자격 증명이 뚫릴 수 있다.

리플레이 공격으로부터 안전한 MAC 로직을 어떻게 구할 수 있을까? 이와 같은 고민은 실생활에서 OTP 가 어떻게 해결했는지를 보면 알 수 있다. 만약 은행 계좌의 OTP 카드 번호가 매번 동일하다면, MITM 은 OTP 카드 번호를 한 번만 탈취한다면 은행 계좌를 해킹할 수 있을 것이다. 각각의 은행 계좌는 인증이 필요할 때마다 해당 인증 때에만 유효한 MAC 을 생성하는 것이 안전하다. 현재의 OTP 들은 counter 또는 현재 timestamp 를 기반으로 일회용 코드를 생성해낸다 (참고 링크).



블록 암호화

블록 암호화는 하나의 키 아래에서 블록 암호를 반복적으로 안전하게 이용하게 하는 절차를 말한다. 블록 암호는 특정한 길이의 블록 단위로 동작하기 때문에, 가변 길이 데이터를 암호화하기 위해서는 먼저 이들을 단위 블록들로 나누어야 하며, 그리고 그 블록들을 어떻게 암호화할지 정해야 하는데, 이때 블록들의 암호화 방식을 운용 방식이라 부른다.

운용 방식은 주로 암호화와 인증을 목적으로 정의되어 왔다. 역사적으로 암호화 방식은 다양한 시나리오의 데이터 수정 측면에서 오류 증식 특성과 관련하여 널리 연구되어 왔다. 나중에 무결성 보호는 암호화와는 완전히 별개로 다루게 되었다. 현대의 일부 운용 방식은 암호화와 인증을 효율적인 방식으로 병합해 놓고 있는데, 이를 인증된 암호 방식(authenticated encryption) 방식으로 부른다. 가장 빈번하게 사용되는 대칭키 블록 암호화로는 AES 가 있다.



AES

AES 에는 3가지 버전이 있다. AES-128, AES-192, AES-256 이다. AES-128 은 16바이트, AES-192 는 24바이트, AES-256 은 32바이트의 대칭키를 사용한다. AES 는 키 길이에 비례한 비트 보안 을 지닌다. AES 암호화는 다음과 같은 특징을 지닌

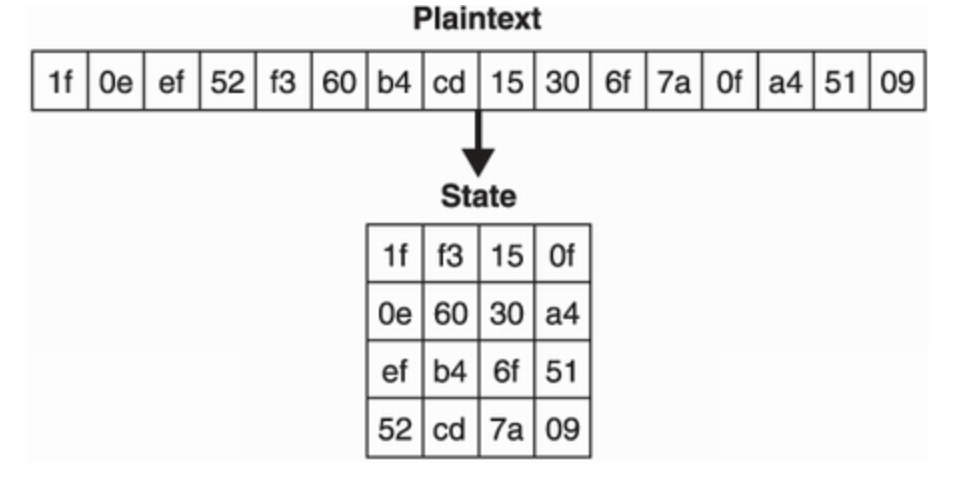
내부적으로는, AES 암호화는 4*4 바이트의 이중 배열로 평문을 암호화한다.

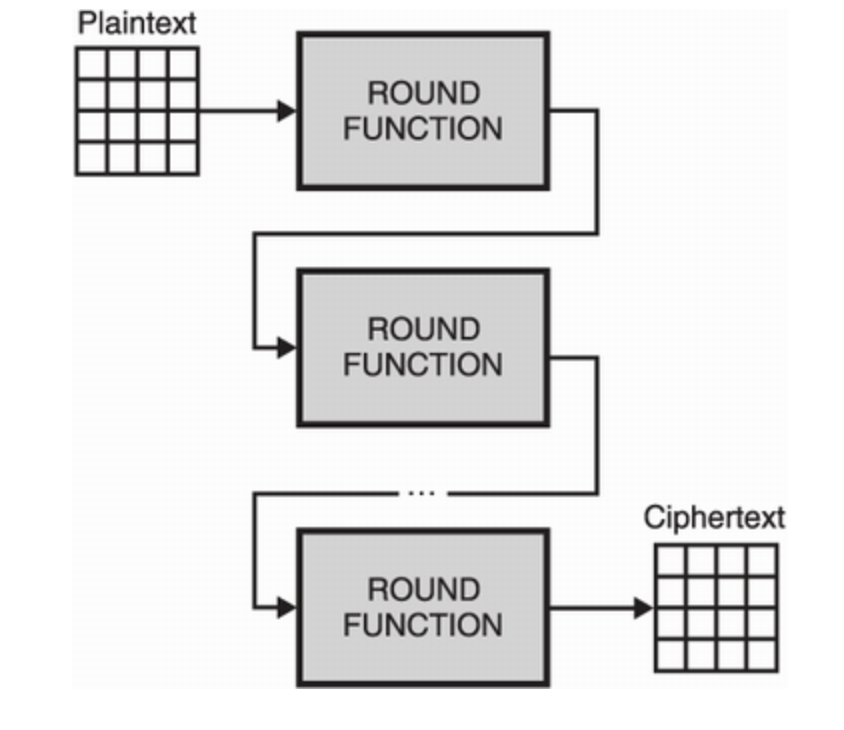
SHA-2 해시 함수와 비슷하게, AES 함수 또한 블록 암호화를 재귀적으로 호출한다. 마찬가지로, IV 값을 주어서 초기화하기도 한다. IV 값을 사용하지 않으면, ECB Penguin 현상이 발생할 수 있다. IV 가 없다면, AES 암호화 함수는 반복하여 실행하면 항상 같은 암호문이 나온다. 각각의 다른 평문을 암호화하다 보면, 암호화의 패턴이 노출될 수 있다.

ECB Penguin. IV 값을 통해 암호문을 랜덤화하지 않는다면, 암호화 로직의 경향성을 추론할 수 있다.

AES 암호화의 운용법으로는 ECB, CBC, CFB, OFB, CTR 가 있지만, 그 중에서 가장 많이 사용되는 CBC 모드에 대해서 살펴보자.

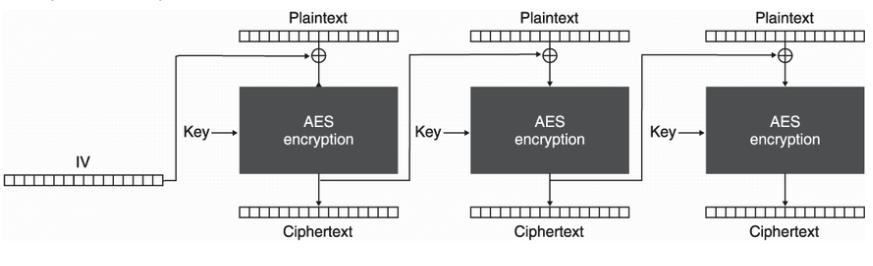
CBC 모드는 암호화 평문을 블록으로 잘라서, 반복적으로 암호화를 실행한다. IV 값을 통해 암호화값의 결과를 랜덤화시킬 수 있다. CBC 모드에서, IV 값은 반복 불가능해야 하고, 예측할 수 없어야 한다. 많은 AES 라이브러리들에서, IV 값들은 예측할 수 없는 랜덤 함수로 구현된다.



키 교환

디피-헬먼 키교환

ECDH 키교환

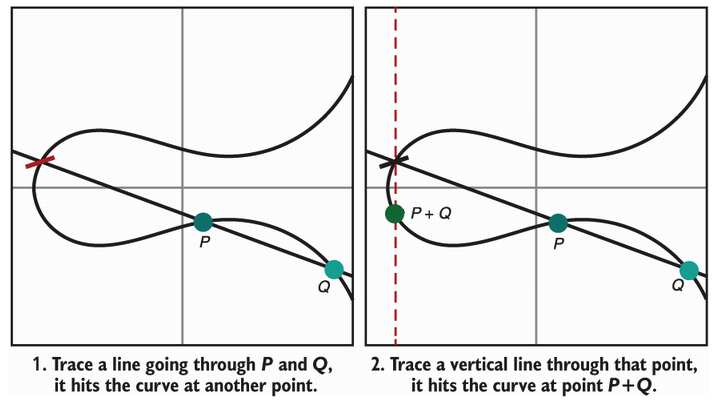
ECDH 키교환은 타원곡선을 사용한다. P 와 Q 가 서로 키교환을 한다고 가정해보자. P 와 Q 를 이은 직선과 타원곡선이 만나는 점 (P+Q) 에서 수직선을 그어, 타원곡선과 만나는 점을 선택한다. P+Q 만으로는 P 와 Q 의 값을 알 수 없지만, P 와 Q 는 각자의 좌표를 알고 있기 때문에, 서로의 좌표를 알 수 있다. 다시 말해, P+Q 와 P 를 알면 Q 를 추론해낼 수 있다. 반대로, P+Q 만 안다고 했을 때, P 와 Q 를 도출해 내는 것은 매우 어렵다.



비대칭 암호화

안전한 대칭키 암호화를 활용하여 많은 안전한 시스템들을 설계할 수 있지만, 분명 대칭키 암호화에는 한계가 있다. 당연하지만, 대칭키가 탈취당하면 모든 보안이 뚫리게 된다는 점이다. 안전한 암호화 과정을 거치려면 키를 안전하게 보관하는 것이 중요하다. 비대칭 암호화는 앞의 키 교환 에 나온 디피-헬먼 키교환과 ECDH 키교환 등의 기법을 활용하여 공개키를 교환한 후, 암호화 메세지를 주고받는 암호화 방식을 일컫는다.

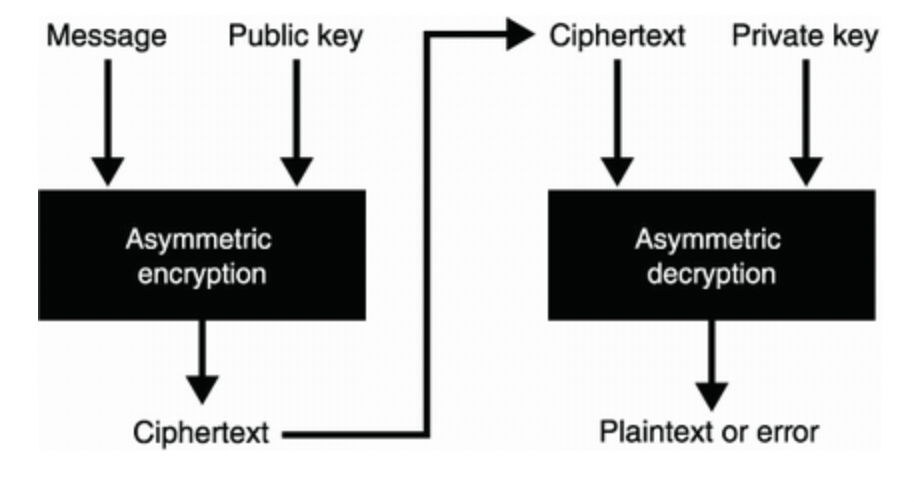
비대칭 암호화는 공유된 공캐키로 평문으로 암호화한 후, 비밀키로 이를 복호화한다.

비대칭 암호화에 대해 처음 공부했을 때에, 풀리지 않는 의문이 있었다. 비대칭키 암호화가 공개키 암호화보다 안전한 것으로 보이는데, 그렇다면 공개키 암호화를 왜 사용할까 ? 였다. 하지만, 비대칭키 암호화 알고리즘은 완전하지 않다. 가장 대표적인 이유는 다음과 같다.

그렇다면, 대칭키 암호화와 비대칭키 암호화의 장점만 취한 암호화 방식은 없을까 ? 이러한 방식에 가장 근접한 방식이 하이브리드 암호화 방식이다. 이름에서 알 수 있듯이, 하이브리드 암호화는 대칭/비대칭 암호화를 모두 활용한 암호화 방식이다.

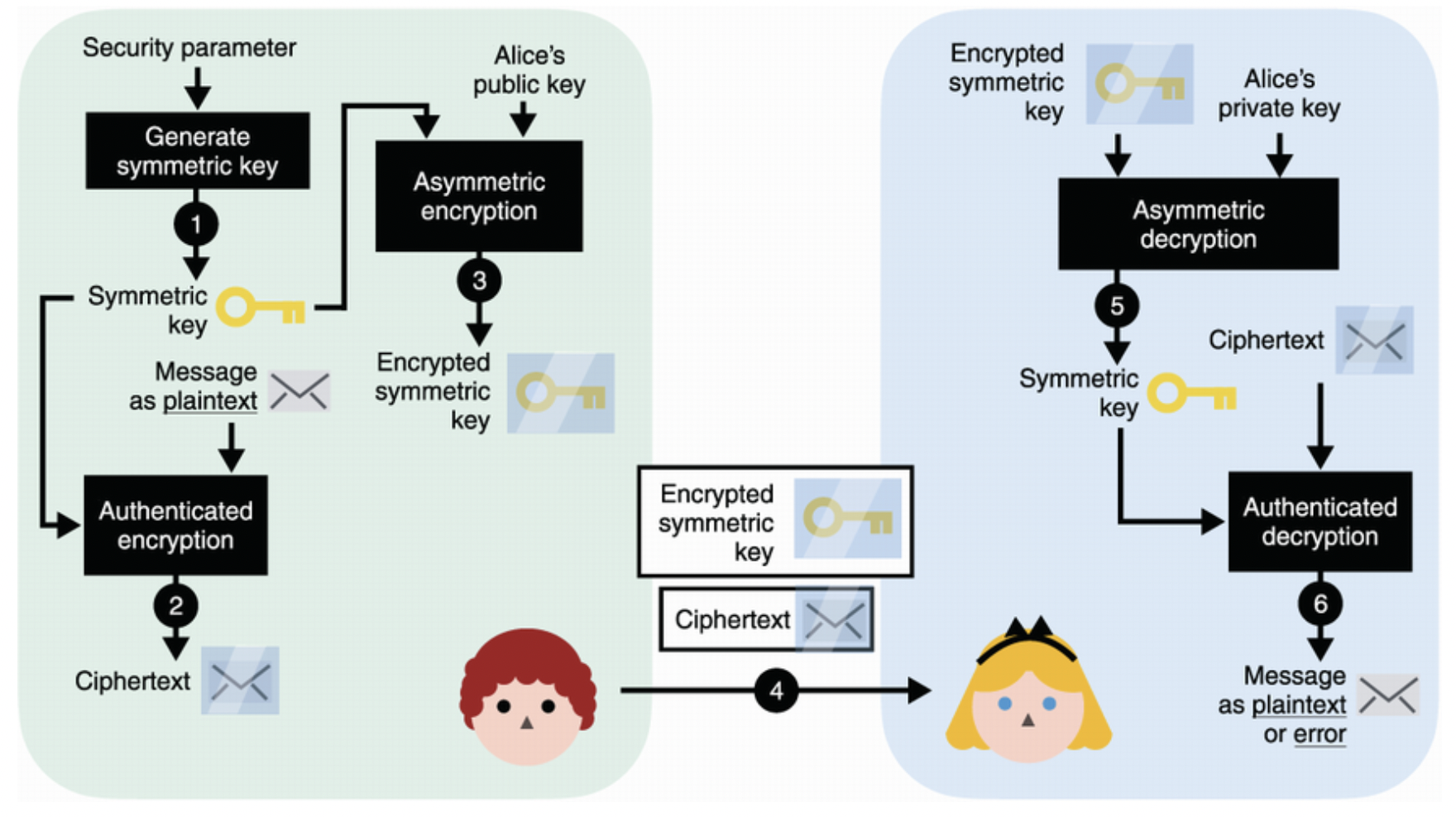
대칭키를 비대칭 암호화를 통해 암호화한 후, 공개키와 함께 전달한다. 복호화할 때에는 비대칭키 복호화를 통해 대칭키를 구한 후, 구한 대칭키로 암호문을 복호화한다.



RSA

RSA 비대칭 암호화는 암호화 표준과 구현 모두에서 많은 취역점과 약점이 발견되었다. 그럼에도 많이 사용되는 비대칭키 암호화이다. 교과서적인 RSA 암호화 방식(Textbook RSA Algorithm)을 간단히 요약하면 다음과 같다.

  1. 두 개의 큰 소수 p 와 q 를 생성한다.t
  2. 임의의 공개 지수 e 를 선택한다. 이 때에 e 는 p-1, q-1 과 서로소여야 한다. 많은 라이브러리들에서는 e 를 소수인 65537 을 사용한다.
  3. 공개키를 유도한다. 공개 키는 e 와 N 이다. N = p * q
  4. 비밀키는 d 이다. d = e^–1 mod (p – 1) (q – 1)
  5. 메시지의 암호화는 message^e mod N 식을 통해 암호화한다.
  6. 암호문의 복호화는 ciphertext^d mod N 을 통해 복호화한다.

교과서적인 RSA 알고리즘이 위험한 이유가 무엇일까 ? 한 가지 예는 작은 메시지 (ex. message = 2) 일 때 발생한다. 0에서 100 사이의 모든 작은 숫자를 암호화하고, 암호화된 숫자가 암호문과 일치하는지 Brute force 방식으로 뚫을 수 있기 때문이다. 이러한 일들로 인해, RSA 암호화 표준은 암호화 전에 비결정론적(Nondeterministic) 패딩을 사용하여 메시지 크기를 최대화한다. 예를 들어, RSA PKCS#1 v1.5 표준은 메시지에 임의의 바이트 수를 추가하는 패딩을 정의한다.

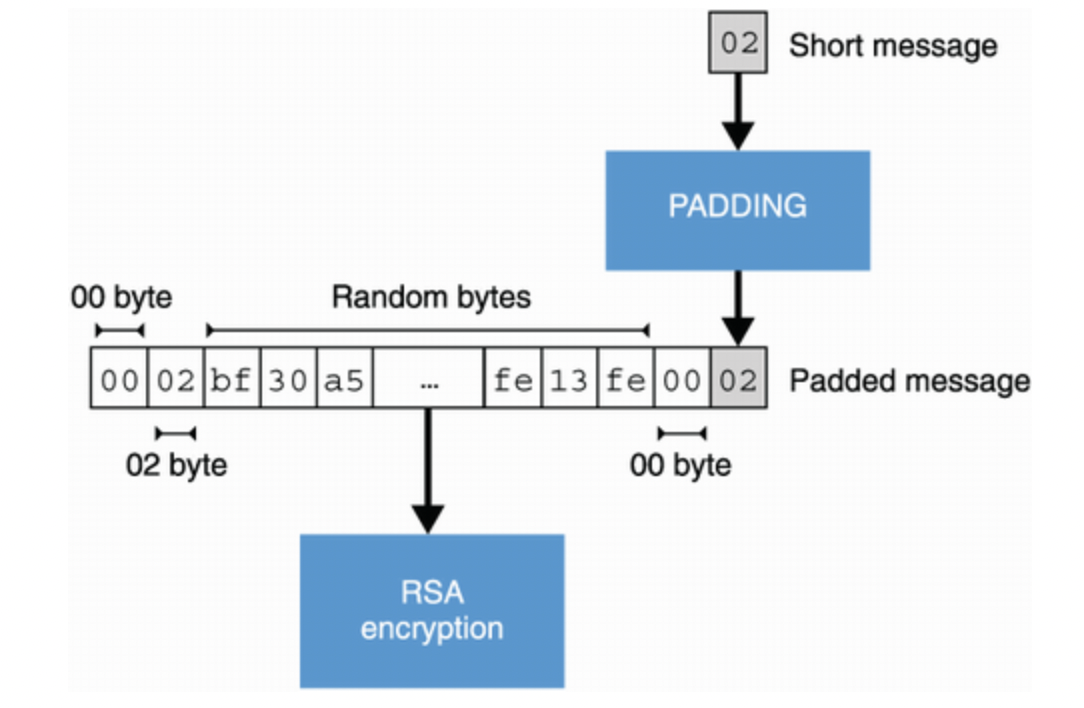
RSA PKCS#1 방식을 사용하면 위와 같은 공격은 막을 수 있지만, RSA PKCS#1 은 적응 선택 암호문 공격(Adaptive Chosen Ciphertext Attack) 에 취약하다고 알려져 있다. 공격 방법을 간단히 요약하면, 공격자는 암호화된 평문을 반복적으로 복호화 로직에 보낸 후, 복호화 로직이 보인 반응을 살피며 귀납적으로 평문을 유추해 나가는 방식이다.

적응 선택 암호문 공격을 방어하려면, 안전한 패딩 방식을 활용한 RSA-OAEP 암호화 방식을 활용할 수 있다.



전자서명

전자서명은 마치 실제 세계의 그것과 유사하다. 다만, 전자서명은 실제 세계의 서명과는 다르게 누가 서명하였는지 알 수 있고, 메세지가 변조되었는지도 파악할 수 있다. 대한민국에서는 공인인증서를 통해 많은 국민들이 전자서명에 익숙하지만, 전자서명은 다양한 분야들에 활용될 수 있다. 가장 간단한 예시로는, 앞에 나타난 키 교환 에 활용될 수 있다. 키 교환 과정에서 MITM 이 중간에 끼어있다면, MITM 이 메세지를 복호화할 수 있게 된다. 다음의 두 케이스를 살펴보면, 전자서명이 어떻게 보안을 높일 수 있는지 알 수 있다.

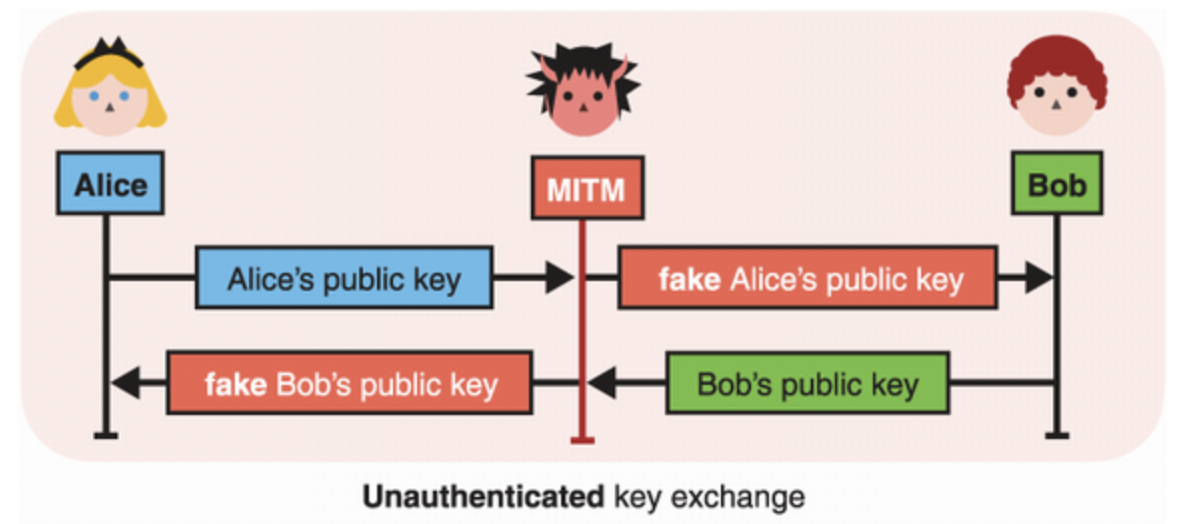
인증되지 않은 키 교환. MITM 의 본인이 생성한 공개 키를 양 쪽의 키 교환에 사용한다면, 앨리스와 밥의 메세지를 모두 복호화할 수 있게 된다.

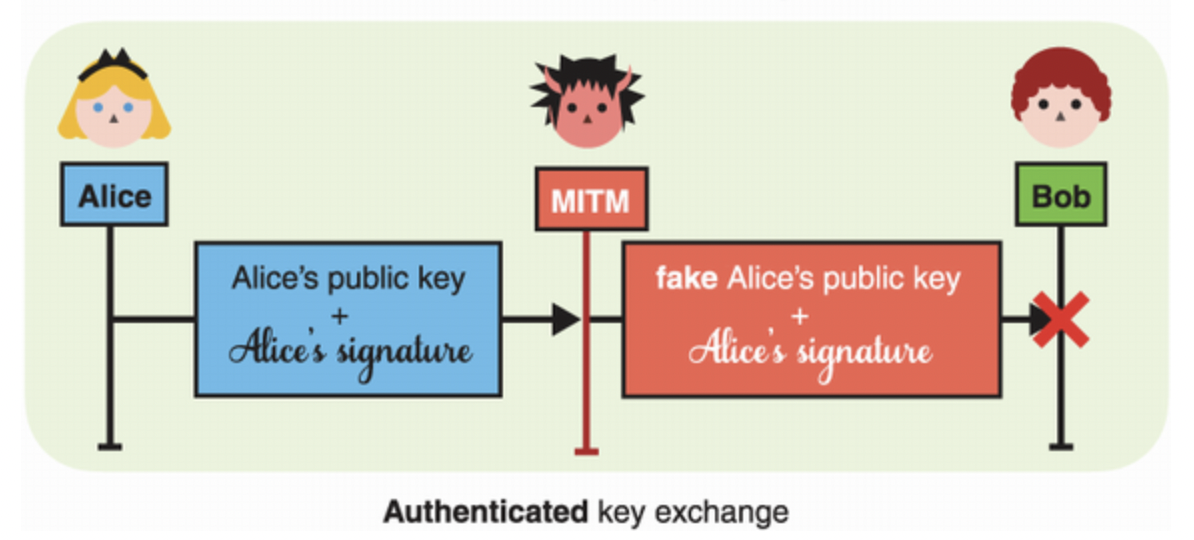
인증된 키 교환. 각자가 공개키에 대한 서명 과정을 거쳤으므로, MITM 이 중간에 메시지를 변조해도 알아차릴 수 있다.

전자서명을 간단하게 추상화하자면, 비대칭키 암호화가 역방향으로 진행된 것이라 볼 수 잇다. 공개키 대신 비밀키로 암호화하며, 공개키로 복호화한다. 공개키로 복호화하였을 때 원하는 결과가 복호화 되었다면, 올바르게 메세지가 전자서명되었다고 볼 수 있다. 전자서명에서 가장 많이 사용되는 알고리즘은 RSA 알고리즘인데, 비대칭 암호화에서 살펴보았듯이, RSA 알고리즘은 보안적으로 안전하지 않다.



Padding

블록 암호화를 사용할 때, 항상 정해진 길이만큼의 데이터를 암호화할 수 있기 때문에, 정해진 길이보다 짧은 데이터를 암호화해야 한다면, 빈 공간만큼 값을 채워넣어 주어야 한다. 가장 흔하게 쓰이는 방식으로는 PKCS#5 와 PKCS#7 가 있다.

PKCS#5

PKCS5 padding 은 RFC 2898 인 "Password-based Encryption Standard" 에 정의된 패딩 방식으로 암호화하려는 데이터가 블록의 배수가 아닐 경우 다음과 같이 부족한 길이만큼 패딩을 하는 방식이다. 예를 들어, 원본 데이타가 AB 라는 값으로 끝나고 8바이트가 블록 사이즈인데 암호화하려는 원본이 17 바이트라면 2개의 블록과 1바이트가 암호화 대상이 된다. 블록 크기만큼 맞추려면 7바이트가 부족하므로 다음과 같이 07 을 7번 패딩한다.

AB 07 07 07 07 07 07 07

3 바이트가 부족할 경우 03 을 3번 패딩하면 된다.

AB A1 08 01 0A 03 03 03

암호화하려는 데이터가 8의 배수라면, "08" 을 8번 반복한다.

08 08 08 08 08 08 08 08

PKCS#7

PKCS#7 padding 은 최대 16 byte 까지의 블록 사이즈에 대해서도 동작하도록 정의한 것만 빼고는 PKCS#5 padding 과 동작 방식이 동일하다. 예를 들어, 블록 사이즈가 128비트 (16바이트) 이고, 마지막 블록이 AB 라는 값으로 끝날 경우, 마지막 블록을 PKCS#7 방식으로 패딩 처리한다면, 다음과 같이 처리된다.

AB 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F

Timing Attack

이것도 읽어보세요